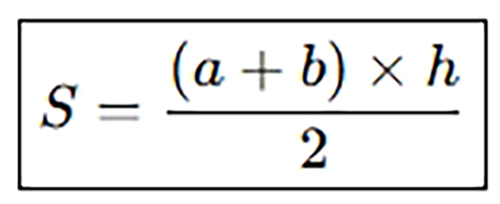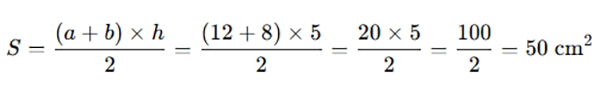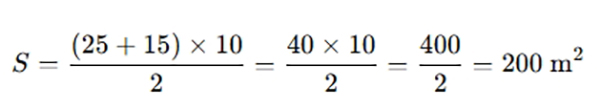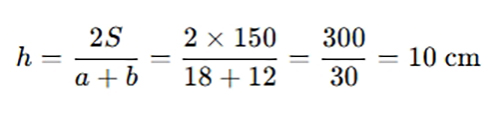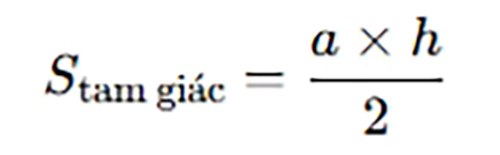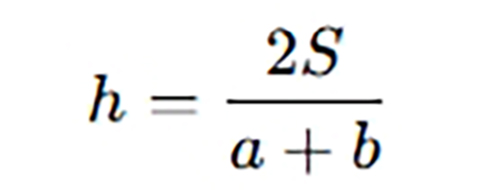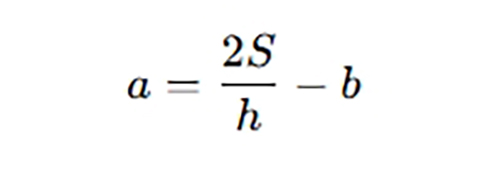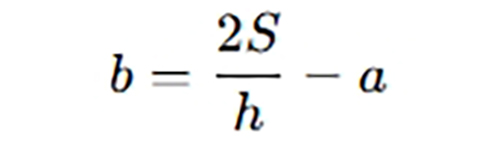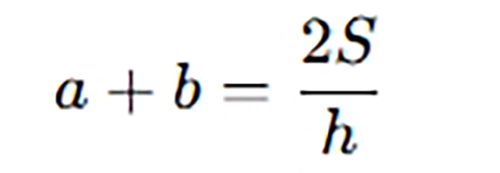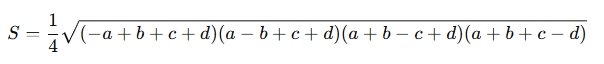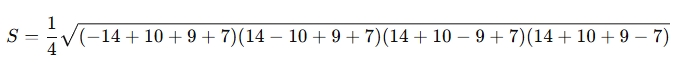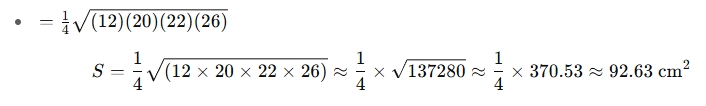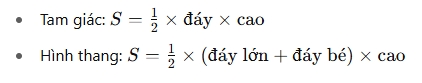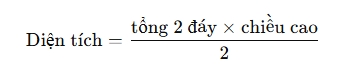Công thức tính diện tích hình thang, chu vi hình thang

Bạn đang học Toán và gặp bài tập yêu cầu tính diện tích hình thang? Bạn chưa nhớ chính xác công thức hoặc không biết cách áp dụng cho đúng? Đừng lo! Trong bài viết này, chúng tôi sẽ giúp bạn hiểu rõ hình thang là gì, cách tính diện tích hình thang nhanh, chính xác và cực kỳ dễ nhớ. Bên cạnh đó là ví dụ minh họa thực tế, mẹo học nhanh công thức và giải đáp những câu hỏi thường gặp. Cùng khám phá nhé!

Giới Thiệu Chung Về Hình Thang

Hình thang là một hình tứ giác đặc biệt trong hình học phẳng, có hai cạnh đối song song gọi là đáy lớn và đáy bé. Hai cạnh còn lại không song song được gọi là cạnh bên. Nhờ cấu tạo này, hình thang trở thành một trong những dạng hình học phổ biến nhất trong chương trình Toán học từ lớp 5 đến lớp 9.

Hình thang được phân loại thành nhiều dạng như:

• Hình thang vuông: Có một góc vuông.

• Hình thang cân: Hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau.

• Hình thang thường: Không vuông và không cân.

Trong thực tế, hình thang xuất hiện rất nhiều như: mặt bàn, mái nhà, mảnh đất ruộng bậc thang, bậc cầu thang,… Việc nắm vững kiến thức về hình thang và cách tính diện tích hình thang không chỉ giúp bạn học tốt môn Toán mà còn hỗ trợ nhiều trong các ngành nghề kỹ thuật, kiến trúc và xây dựng.

Công Thức Tính Diện Tích Hình Thang Chuẩn Nhất

Để tính diện tích hình thang, bạn chỉ cần nhớ một công thức duy nhất, áp dụng được cho mọi loại hình thang – dù là vuông, cân hay thường:

​​

Trong đó:

• S là diện tích hình thang

• a là độ dài đáy lớn

• b là độ dài đáy bé

• h là chiều cao – khoảng cách vuông góc giữa hai đáy

Ghi nhớ đơn giản: “Tổng hai đáy nhân với chiều cao, chia hai ra ngay diện tích.”

Đây là công thức được áp dụng rộng rãi trong chương trình toán học lớp 5, lớp 7 và trong các bài kiểm tra, đề thi học sinh giỏi, thi tuyển sinh.

Lưu ý: Dù hình thang có hình dạng thế nào đi nữa (cân, vuông, lệch…), chỉ cần xác định đúng đáy lớn, đáy bé và chiều cao là có thể áp dụng công thức tính diện tích chính xác.

Ví Dụ Minh Họa Cụ Thể

Ví dụ 1: Tính diện tích hình thang đơn giản

Đề bài:

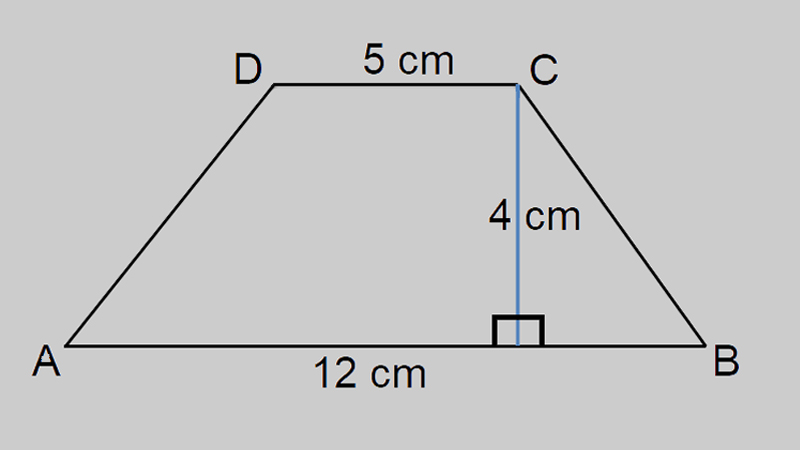
Một hình thang có:

• Đáy lớn a = 12 cm 

• Đáy bé b = 8 cm 

• Chiều cao h = 5 cm 

Áp dụng công thức:

👉 Kết luận: Diện tích hình thang là 50 cm²

Ví dụ 2: Bài toán thực tế

Đề bài: Một mảnh đất hình thang có đáy lớn dài 25m, đáy bé dài 15m và chiều cao là 10m. Hỏi diện tích mảnh đất đó là bao nhiêu?

Lời giải:

👉 Đáp số: Diện tích mảnh đất là 200m²

Ví dụ 3: Tính chiều cao khi biết diện tích và hai đáy

Đề bài: Một hình thang có đáy lớn $=18$ cm, đáy bé $=12$ cm, diện tích là S =150 cm². Hỏi chiều cao của hình thang là bao nhiêu?

Áp dụng công thức biến đổi:

Kết luận: Chiều cao của hình thang là 10 cm

Mẹo Ghi Nhớ Công Thức

Để học thuộc nhanh công thức tính diện tích hình thang, bạn có thể áp dụng các mẹo sau:

1. Vần điệu dễ thuộc:

“Tổng hai đáy nhân chiều cao, chia đôi ra ngay kết quả.”
Vừa có vần, vừa có nhịp – dễ học, dễ nhớ, cực hiệu quả cho học sinh tiểu học và THCS.

2. Hình ảnh hóa công thức

Hãy tưởng tượng hình thang như một hình chữ nhật bị vát chéo hai đầu. Khi cộng đáy lớn và đáy bé lại, rồi chia đôi, bạn đang tính độ dài trung bình của đáy, sau đó nhân với chiều cao để ra diện tích — giống như diện tích hình chữ nhật thông thường.

3. So sánh với công thức hình tam giác

Nếu bạn đã thuộc công thức tính diện tích tam giác:

Thì diện tích hình thang chỉ khác ở chỗ thay “a” bằng “(a + b)”, vì hình thang có hai đáy thay vì một.

Các Trường Hợp Đặc Biệt Của Hình Thang

Trong hình học, hình thang có thể chia thành nhiều loại khác nhau tùy theo đặc điểm cạnh, góc hoặc tính đối xứng. Dưới đây là các trường hợp đặc biệt thường gặp:

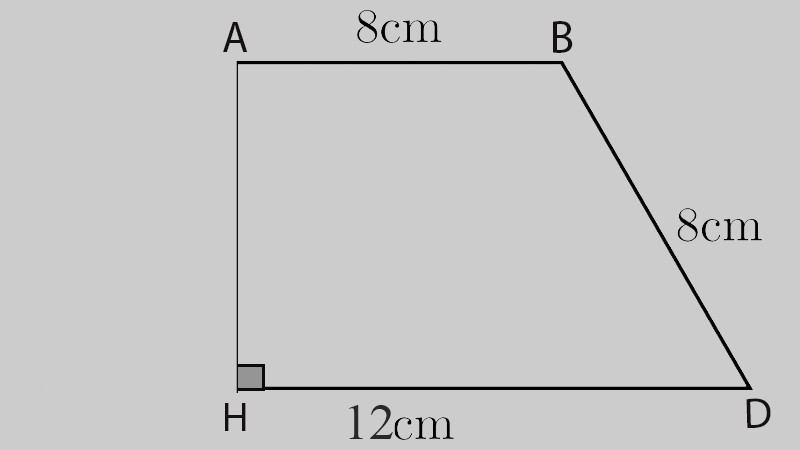
Hình Thang Vuông

Đặc điểm nhận biết:

• Có một góc vuông (90 độ).

• Một cạnh bên vuông góc với hai đáy.

Ứng dụng: Xuất hiện nhiều trong thực tế như: cầu thang, lan can, mái dốc vuông.

Lưu ý: Vì có chiều cao chính là cạnh bên vuông góc, nên việc xác định chiều cao và áp dụng công thức rất đơn giản:

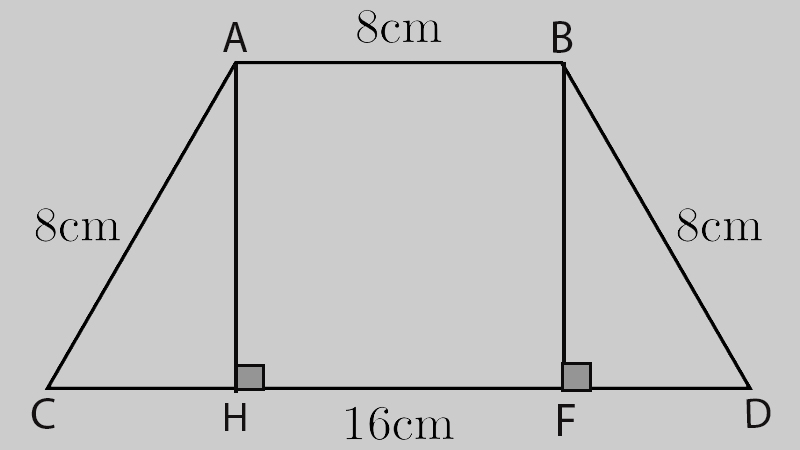
Hình Thang Cân

Đặc điểm nhận biết:

• Hai cạnh bên bằng nhau.

• Hai góc kề đáy bằng nhau.

• Trục đối xứng đi qua trung điểm hai đáy.

Ứng dụng:

• Thường gặp trong thiết kế đối xứng: cửa sổ, lan can, họa tiết kiến trúc,…

Lưu ý: Chiều cao được vẽ từ trung điểm một đáy xuống đáy kia, có thể áp dụng định lý Pitago nếu biết độ dài cạnh bên.

Hình Thang Thường

Đặc điểm nhận biết:

• Không có góc vuông.

• Hai cạnh bên không bằng nhau.

• Không đối xứng.

Ứng dụng:

• Mảnh đất, bãi cỏ, các thiết kế không đều hai bên.

Lưu ý: Vẫn áp dụng công thức chuẩn:

Việc nắm rõ từng loại hình thang giúp bạn:

• Nhận diện đúng dạng đề bài

• Xác định chiều cao chính xác

• Vận dụng công thức hiệu quả hơn

Công Thức Biến Đổi Theo Từng Dạng

Ngoài công thức chuẩn để tính diện tích hình thang:

Chúng ta còn có thể biến đổi linh hoạt công thức này để tính các yếu tố còn lại như: chiều cao, một trong hai đáy hoặc kiểm tra dữ kiện.

Tính chiều cao khi biết diện tích và hai đáy

📌 Dùng khi đề bài cho biết diện tích và độ dài hai đáy, cần tìm chiều cao.

2. Tính đáy lớn khi biết diện tích, đáy bé và chiều cao

📌 Dùng khi biết đáy bé, chiều cao và diện tích, cần tìm đáy còn lại.

3. Tính đáy bé khi biết diện tích, đáy lớn và chiều cao

📌 Tương tự như trên, đổi vị trí đáy cần tìm.

4. Tính tổng hai đáy

📌 Dùng trong các bài toán suy luận hoặc so sánh tổng hai đáy khi biết diện tích và chiều cao.

Công thức tính chu vi hình thang

Ngoài diện tích, chu vi cũng là yếu tố quan trọng khi làm việc với hình thang, đặc biệt trong các bài toán yêu cầu tính độ dài đường rào, khung viền hay vật liệu xây dựng.

Công thức chung: P = a + b + c + d 

Trong đó:

• a: Đáy lớn

• b: Đáy bé

• c và d: Hai cạnh bên

• P: Chu vi hình thang (tổng độ dài 4 cạnh)

Ví dụ minh họa:

Đề bài: Một hình thang có:

• Đáy lớn $=14$ cm

• Đáy bé $=10$ cm

• Cạnh bên $=6$ cm và $=5$ cm

Tính chu vi hình thang?

Lời giải:

P = a + b + c + d = 14 + 10 + 6 + 5 = 35 cm

Đáp án: Chu vi hình thang là 35 cm

Công thức tính diện tích hình thang khi biết độ dài 4 cạnh

Trong trường hợp bạn không biết chiều cao, nhưng biết đủ cả 4 cạnh của hình thang (2 đáy và 2 cạnh bên), bạn có thể áp dụng công thức tính diện tích theo độ dài 4 cạnh.

Công thức (theo công thức Brahmagupta cải biên):

Trong đó:

• a và $b$: độ dài hai đáy

• c và $d$: độ dài hai cạnh bên

• S: diện tích hình thang

Lưu ý: Công thức này chỉ áp dụng cho hình thang lồi, và khi các cạnh tạo thành tứ giác có thể vẽ được. Trong thực tế, việc dùng công thức này khá phức tạp và hiếm gặp trong chương trình phổ thông, chủ yếu dành cho toán nâng cao hoặc chuyên đề.

📘 Ví dụ minh họa:

Đề bài: Một hình thang có 4 cạnh lần lượt là:

• Đáy lớn $=14$ cm

• Đáy bé $=10$ cm

• Cạnh bên $=9$ cm và $=7$ cm

Tính diện tích hình thang.

Áp dụng công thức:

Tính toán từng phần:

Đáp án: Diện tích hình thang xấp xỉ 92.63 cm²

Khi nào nên dùng công thức này?

• Khi không có chiều cao và không thể tính được chiều cao bằng lượng giác hay tam giác vuông.

• Khi đề bài yêu cầu cụ thể sử dụng 4 cạnh.

• Trong các bài toán nâng cao hoặc chuyên đề hình học lớp 9 – lớp 10.

Ứng Dụng Thực Tế Của Diện Tích Hình Thang

Việc học công thức tính diện tích hình thang không chỉ phục vụ cho môn Toán học, mà còn có rất nhiều ứng dụng thực tế trong đời sống, xây dựng, thiết kế và các ngành kỹ thuật.

1. Tính diện tích mảnh đất không vuông vức

Nhiều thửa đất ngoài thực tế có hình dáng không đều, thường là hình thang (một cạnh trước rộng, cạnh sau hẹp). Để tính diện tích đất chính xác, ta dùng:

Ví dụ: Mảnh đất hình thang có chiều rộng trước 10 m, sau 6 m, chiều dài 20 m → dễ dàng tính diện tích để mua bán, xây dựng.

2. Ứng dụng trong xây dựng & kiến trúc

• Tính diện tích mái nhà nghiêng, bậc cầu thang, mái hiên hình thang

• Thiết kế mặt cắt vát trong bản vẽ kỹ thuật (giống hình thang)

• Dự toán vật liệu cần dùng cho phần khung viền, lát gạch,…

3. Thiết kế thời trang & mỹ thuật

• Vẽ hoặc thiết kế túi xách, váy, cổ áo, khung tranh theo hình thang

• Cắt may chính xác cần tính diện tích vải theo mẫu hình học

4. Kỹ thuật giao thông

• Tính diện tích mặt cắt đường (nhiều đoạn có hình thang do độ dốc)

• Thiết kế đường dốc, đoạn chuyển tiếp giữa hai độ cao

5. Trắc địa – đo đạc bản đồ

• Đo và tính diện tích khu vực không vuông vức bằng cách chia nhỏ thành hình thang

• Áp dụng công thức diện tích để xử lý số liệu đo đạc nhanh chóng

6. Ứng dụng trong giáo dục

• Là bài toán thực tế phổ biến trong chương trình Toán lớp 5, lớp 7

• Giúp học sinh hình dung việc học Toán không chỉ để làm bài thi, mà còn giải quyết vấn đề thực tiễn

Câu Hỏi Thường Gặp (FAQ)

1. Công thức tính diện tích hình thang là gì?

Công thức chuẩn là:

Trong đó:

• a: đáy lớn

• b: đáy bé

• h: chiều cao (vuông góc giữa 2 đáy)

• S: diện tích hình thang

2. Làm sao để tính diện tích khi chỉ biết 4 cạnh?

Bạn dùng công thức đặc biệt (dành cho nâng cao):

Áp dụng khi biết đầy đủ 4 cạnh (2 đáy và 2 cạnh bên) mà không biết chiều cao.

3. Làm sao để phân biệt đáy lớn và đáy bé?

Hai cạnh song song trong hình thang là hai đáy.

• Đáy có độ dài lớn hơn là đáy lớn (ký hiệu: a)

• Đáy nhỏ hơn là đáy bé (ký hiệu: b)

4. Có những loại hình thang nào?

Gồm 3 loại chính:

• Hình thang thường: không cân, không vuông

• Hình thang vuông: có 1 góc vuông

• Hình thang cân: hai cạnh bên bằng nhau, hai góc đáy bằng nhau

5. Chiều cao của hình thang là gì? Lấy ở đâu?

Chiều cao là khoảng cách vuông góc giữa hai đáy.

• Nếu hình thang vuông: chiều cao = cạnh bên vuông

• Nếu không có sẵn: phải tính bằng lượng giác, định lý Pitago hoặc đo đạc thực tế

6. Diện tích hình thang có giống diện tích hình tam giác không?

Không giống, nhưng có điểm tương đồng:

→ Hình thang có 2 đáy nên cần lấy trung bình cộng trước khi nhân với chiều cao.

7. Khi nào cần chia đôi trong công thức?

Luôn chia đôi vì công thức tính diện tích hình thang dựa trên trung bình cộng của hai đáy:

8. Nếu không biết chiều cao thì có tính được diện tích không?

Có thể, nhưng cần thêm thông tin khác như:

• Độ dài hai cạnh bên và góc

• Dùng công thức đặc biệt khi biết 4 cạnh (nâng cao)

Hashtag: #CôngThứcToánHọc #DiệnTíchHìnhThang #HọcToánLớp7 #KiếnThứcPhổThông #ToánHọcThựcTế #CáchTínhDiệnTích #ToánHọcCơBản #HìnhHọcPhẳng #BàiTậpToán